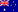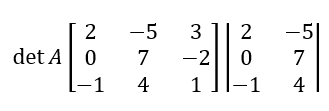ติวคณิตคอม

ดีเทอร์มิแนนท์ของเมตริกซ์ (determinant)  คือ ค่าหรือตัวเลขที่ได้จากการปฏิบัติการภายในสมาชิกของ เมตริกซ์ ซึ่งจะเป็นเมทริกซ์จัตุรัสเท่านั้น คือ จำนวนแถว และหลักเท่ากัน

ดีเทอร์มิแนนท์ของ A จะเขียนแทนด้วยสัญลักษณ์ “det A” หรือ “|A|” 

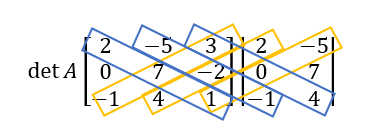
How to find the determinant of a 3x3 matrix

จากการเรียนวิชาคณิตศาสตร์คอมพิวเตอร์เรื่องเมทริกซ์ จะพบวิธีการหา ดีเทอร์มิแนนต์ 2 วิธี ที่แตกต่างกันแต่ได้ผลลัพธ์เหมือนกัน คือ 

Exercises on evaluating the determinant of a 3x3 matrix

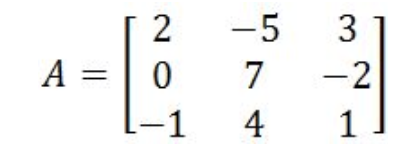
ต้องมีการนำ  2  หลักแรกของดีเทอร์มิแนนท์มาเขียนต่อไว้ทางขวามือของดีเทอร์มิแนนท์เดิม  ดังนี้

det(A)   =   ( 2x7x1 + (-5)x(-2)x(-1) + 3x0x4) -  ((-1)x7x3 + 4x(-2)x2 + 1x0x(-5))

           =     (  14 + (-10) +   0 )  –  (-21)+ (-16) + 0)

           =             4   –  (-37) เปลี่ยนลบเป็นบวกด้วยจำนวนตรงข้ามของ (-37)

           =         4+37

           =           41

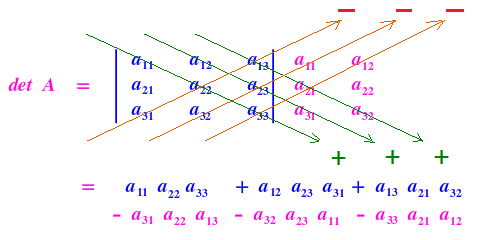
จากโจทย์

 det(A)   =   ( 2x7x1 + (-5)x(-2)x(-1) + 3x0x4) -  ((-1)x7x3 - 4x(-2)x2 - 1x0x(-5))

           =     (  14 + (-10) +   0 )  –  (-21) - (-16) - 0)

           =             4   –  (-21)  - (-16) เปลี่ยนลบเป็นบวกด้วยจำนวนตรงข้ามของ (-21)

           =        25-(-16)  เปลี่ยนลบเป็นบวกด้วยจำนวนตรงข้ามของ (- 16)

           =           41

สรุป แม้วิธีการคิดจะแตกต่างกัน แต่สามารถหาผลลัพธ์ได้เท่ากัน น้อง ๆ สามารถหาเลือกใช้วิธีใดในการหาคำตอบก็ได้เนื่องจากในห้องสอบนั้น เราต้องใช้วิธีการที่เหมาะกับเราและง่ายที่สุดเพื่อให้ประหยัดเวลาในการทำข้อสอบนั้นเอง